Regularización
Un aspecto importante en machine learning es hacer que los algortimos funcionen bien para los nuevos datos nunca vistos. Esto se conoce como regularización. Es muy importante tenerlo en cuenta porque los datos de entrenamiento de los que disponemos son limitados y queremos que nuestro algortimo generalize bien para nuevos datos.
Las tecnicas de regualarización aplican técnicas para reducir el error en los nuevos datos a espensas de no reducirlo tanto en los datos de entrenaminto. Cuando una algoritmo se aprende demasiado los datos de entrenaminto, llegando incluso a casi memorizarlos, y no generaliza bien, se conoce como overfitting.
Existen muchas técnicas de regularización:
- Early stopping
- Dropout layer
- Dataset augmentation
- Weight penalty L1 and L2
Early stoping
Parar antes de que empieze el overfitting
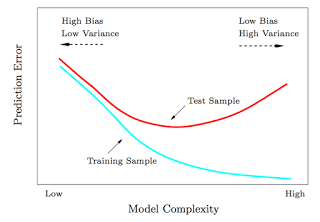
Entender lo de Bias vs Variance tradeoff Coursera
Modificar la función de coste (Parameter Norm Penalties)
Tener una nueva función de coste regularizada J'() a partir de la función de coste original J(),
en la que se penalice también que los parámetros sean muy grandes Ω(θ) (parameter Norm Penalty).
Ademas tiene un parámetro α para ajustar la cantidad en que afecta esta nueva penalización.
J'() = J() + α·Ω(θ)
Nótesese que los parámetros de la red son los pesos y los bias θ = w ∪ b.
Pero sin nos fijamos, los pesos son much más subceptibles de tener overfiting que los bias.
Porque un peso especifica como intercatuan 2 variables, luego necesita muchos datos para observar esas variables en gran varieded de condiciones.
En cambio los bias necesitan muchos menos datos para ajustarse correctamente,
porque especifican como interactúa una varible con toda la capa anterior, por lo tanto no suelen regularizarse.
E incluso si se regularizan los bias puede resultar en underfitting.
Es conveniente usar una penalización diferente, modeificando α, en cada capa.
Regularización L2
Aquí el parametro de penalización se conoce como weight decay. Este técnica lleva a los pesos cerca de su origen ¿?¿?¿?